IKL
Infinite and Multiple Kernel Learning algorithm for Matlab

Introduction
Discrete graph
Quality function for a set of kernel parameters (click to enlarge).

With the multiple kernel learning (MKL) framework it is possible to learn linear combinations of a predefined finite set of kernels. The final kernel is of the form

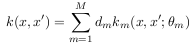
Discrete graph

This can be extended to more general kernel classes which can be even infinite dimensional, e.g. all Gaussian kernels with positive definite covariance matrix. With propose the Infinite Kernel Learning (IKL) algorithm to solve this extended problem (see here for a note on the name). For a given class of kernels Θ this approach requires the following (non-convex) problem

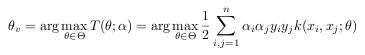
Discrete graph

which is also called subproblem in this context. In our implementation we simply solve it using gradient descent.

The algorithm alternates between two different parts A) a MKL solver and B) a solver for the subproblem. The solver for the subproblem has to be designed specific to the kernel class. For part A) one can reuse any efficient MKL solver and we implemented SimpleMKL.

On this webpage we provide the source code and an example run of the algorithms. As an example class of kernels we implemented the Gaussian kernel but the code is modular such that one can easily substitute with different classes. Since the MKL solver SimpleMKL is used as a part of our algorithm we implemented this formulation. Our implementation is a mixture of the state-of-the-art interior point solver Ipopt and the well known SVM solver libsvm.

Please see the publications section for published papers.

Important note. Subsequent to publication of our Technical Report, we have learnt that similar work has independently been done by S.Özöğür-Akyüz and G.W. Weber e.g. this paper from 12/18/07. In the paper Learning with Infinitely Many Kernels via Semi-Infinite Programming (see also Publications) the name Infinite Kernel Learning is also used to refer to the formulation of the problem rather than the algorithm. We apologize for any confusion this may cause.

Features and Demo

The provided code offers the following functionalities:

Most of the code is written in Matlab and interfaces to LIBSVM and Ipopt.

SimpleMKL Example The following screen capture shows the output when the included simplemkl_example.m file from the distribution is run.

>> simplemkl_example
generating training and test data...press key
using 9 different kernels

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Common Public License (CPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************

MKL: calls F:30,SVM:30,dF:29
Algorithm selected 3 kernels
test accuracy: 0.912
most active kernel (w=0.5) = 10.06
press key to exit

IKL Example The following screen capture shows the output when the included ikl_example.m file from the distribution is run.

>> ikl_example
generating training and test data...press key
SP: generated 1 Gram matrices
SP: generated 64 start_points

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Common Public License (CPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************

IKL: IpOpt iter 2,Calls F:1, dF:2,obj: 149.31,rel.decrease: Inf (thresh 0.00001)
SP: IpOpt iter 22, Evaluations: F:21, dF:22, H:22, Computations needed: 22
found violating constraint...adding it to the constraint set
next factors 0.338 0.238 0.000 9.911 0.194 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.170 0.000 0.172 0.000
SP: found maximum of 1 constraints, returning
current w: 1.000000
IKL: IpOpt iter 9,Calls F:8, dF:9,obj: 148.39,rel.decrease: 0.00613 (thresh 0.00001)
SP: IpOpt iter 22, Evaluations: F:21, dF:22, H:22, Computations needed: 22
.
.
.
.
SP: IpOpt iter 22, Evaluations: F:26, dF:22, H:22, Computations needed: 24
SP: IpOpt iter 22, Evaluations: F:21, dF:22, H:22, Computations needed: 22
SP: IpOpt iter 13, Evaluations: F:12, dF:13, H:13, Computations needed: 13
found violating constraint...adding it to the constraint set
next factors 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 9.724 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.507 0.000
SP: found maximum of 1 constraints, returning
current w: 0.977043 0.011565 0.004898 0.003383 0.003111
IKL: IpOpt iter 22,Calls F:36, dF:22,obj: 9.2664,rel.decrease: 0.00000 (thresh 0.00001)
IKL: Algorithm terminated beracuse 'Objective change smaller than threshold'
final w = : 0.9769 0.0116 0.0049 0.0034 0.0032 0.0001
IKL: #subproblem calls: 13
Algorithm selected 6 kernels
test accuracy: 1
parameters of most active kernel (w=0.98) = 0.96 6.28 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
press key to exit

Download

The software for both SimpleMKL and our Infinite Kernel Learning algorithm can be downloaded below. The package includes the source code, pre-compiled binaries for the Linux/x86 and the Linux/x86-64 architectures. For each method there is an example file demonstrating its usage.

Distribution: source code, pre-compiled binaries and demo files

License: The software is licensed under the BSD License A copy of the license documents is included in the distribution.

Installation: Please read the file INSTALL of the package for detailed installation instruction. If you have the frequently encountered problem complaining about GCC_3.3 not being found when you run the mex functions, please refer to this discussion at the Mathworks forums.

Publications

Contact

If you have comments or questions, please feel free to contact us. Thanks!