Superquadric Glyphs for Symmetric Second-Order Tensors

We currently do not provide an out-of-the-box demo program for our Vis 2010 paper on superquadric tensor glyphs [SK10], but the essential C code is available in the open source library Teem. With the help of this tutorial, you should be able to integrate our code directly into your own favorite visualization framework.

If you are new to Teem, you may find our quick introduction helpful. If you are unfamiliar with OpenGL and GLSL, the books by Shreiner [Shr09] and Rost et al. [RLC09] are standard references. If you should run into problems with this tutorial or if you find an error, Teem’s mailing list is the most useful place for discussing that.

Creating Your First Tensor Glyph

Teem represents symmetric tensors as arrays of seven floating point numbers. The first is a confidence value, which is expected to be in interval [0,1] and can be used to mask parts of a tensor field. It is not relevant to this tutorial. The remaining values specify the unique tensor components, in lexicographic order: xx, xy, xz, yy, yz, zz.

To create a tensor glyph with Teem, you first need to

#include <teem/ten.h>

near the top of your source file. Before geometry is created, we will perform a spectral decomposition of the tensor, map its eigenvalues to normalized (u,v) space (cf. Section 4.2 of the paper), and map (u,v) to the (alpha,beta) parameters of the superquadric (cf. Section 4.3). If the given tensor has very small norm, we will also blend (alpha,beta) with (1,1), so that a sphere will be used as the base glyph of the zero tensor. These steps are done by the following code:

/* input variables */
double ten[7]={1.0,1.0,0.0,0.0,-0.5,0.0,-0.3}; /* tensor coefficients */
double eps=1e-4; /* small value >0; defines the smallest tensor
                  * norm at which tensor orientation is still meaningful */

/* example code starts here */
double evals[3], evecs[9], uv[2], abc[3], norm;

tenEigensolve_d(evals, evecs, ten);
tenGlyphBqdUvEval(uv, evals);
tenGlyphBqdAbcUv(abc, uv, 3.0);
norm=ELL_3V_LEN(evals);
if (norm<eps) {
  double weight=norm/eps;
  abc[0]=weight*abc[0]+(1-weight);
  abc[1]=weight*abc[1]+(1-weight);
  abc[2]=weight*abc[2]+(1-weight);
}

If your goal is to render a large number of glyphs, you should use the (alpha, beta) values as an index into a palette of precomputed base geometries, in order to achieve higher framerates. Details on this strategy will be given in the following section. For now, we’ll pretend that we’re interested in rendering just this one tensor glyph. Let’s first create the base geometry:

/* input variable */
int glyphRes=20; /* controls how fine the tesselation will be */

/* example code starts here */
limnPolyData *lpd = limnPolyDataNew();
limnPolyDataSpiralBetterquadric(lpd, (1 << limnPolyDataInfoNorm),
                                abc[0], abc[1], abc[2], 0.0,
                                2*glyphRes, glyphRes);
limnPolyDataVertexNormals(lpd);

The result will be a superquadric, represented as a single triangle strip. However, it is only the base geometry and has to be rotated and re-scaled to become a tensor glyph:

double absevals[3];
for (int k=0; k<3; k++)
  absevals[k]=fabs(evals[k]);
double trans[16]={absevals[0]*evecs[0], absevals[1]*evecs[3],
                  absevals[2]*evecs[6], 0,
                  absevals[0]*evecs[1], absevals[1]*evecs[4],
                  absevals[2]*evecs[7], 0,
                  absevals[0]*evecs[2], absevals[1]*evecs[5],
                  absevals[2]*evecs[8], 0,
                  0, 0, 0, 1};
unsigned int zone=tenGlyphBqdZoneUv(uv);
if (0==zone || 5==zone || 6==zone || 7==zone || 8==zone) {
  /* we need an additional rotation */
  double ZtoX[16]={ 0,0,1,0,
                    0,1,0,0,
                   -1,0,0,0,
                    0,0,0,1 };
  ell_4m_mul_d(trans, trans, ZtoX);
}
double gltrans[16];
ELL_4M_TRANSPOSE(gltrans, trans); /* OpenGL expects column-major format */

If you’re using OpenGL, it is now straightforward to multiply the modelview matrix by gltrans, and render the base geometry using glDrawElements. If you look at the definition of limnPolyData in teem/limn.h, you will find that xyzw are the vertex positions, norm the normals, and indx is the index array. You should enable GL_NORMALIZE for correct lighting. Culling backfaces will give some speedup, but you probably won’t notice the difference when rendering only a single glyph.

Depending on your camera settings, this is how a rendering of the glyph geometry we created up to this point might look.

Using a Palette of Base Shapes

When your goal is to display thousands of glyphs, generating geometry from scratch for each one of them takes a considerable amount of memory and processing. An optimization described in Section 4.6 of our paper is to pre-compute representative base shapes by a uniform sampling in superquadrics space: Since superquadrics change smoothly with (alpha,beta), neighboring shapes become visually indistinguishable once the sampling is fine enough.

This detail of our palette illustrates that immediately neighboring base shapes are visually equivalent.

The following code creates a 2D array of base glyphs. It has a builtin heuristic to generate the hybrid superquadric that is introduced for better visual continuity in Section 4.3 of our paper. To create tensor glyphs from these base shapes, you would simply render the precomputed geometry that is closest to the (alpha,beta) values that correspond to the eigenvalues (found as above). Note that each tensor still defines its own modelview matrix for proper scaling and orientation of the base shape.

const unsigned int paletteRes=15;
float abc[3];
limnPolyData *lpds[paletteRes][3*paletteRes];
for (unsigned int bIdx=0; bIdx<3*paletteRes; bIdx++) {
  abc[1] = bIdx/(paletteRes-0.333);
  for (unsigned int aIdx=0; aIdx<paletteRes; aIdx++) {
    abc[0] = aIdx/(paletteRes-1.0);
    float dist=sqrt(abc[0]*abc[0]+(abc[1]-3.0)*(abc[1]-3.0));
    if (dist>1.0)
      abc[2]=abc[1];
    else
      abc[2]=(1.0-dist)*2+dist*abc[1];

    lpds[aIdx][bIdx] = limnPolyDataNew();
    limnPolyDataSpiralBetterquadric(lpds[aIdx][bIdx],
                                    (1 << limnPolyDataInfoNorm),
                                    abc[0], abc[1], abc[2], 0.0,
                                    2*glyphRes, glyphRes);
    limnPolyDataVertexNormals(lpds[aIdx][bIdx]);
  }
}

For simplicity, we sample a rectangular part of (alpha, beta) space. Our glyphs only make use of a subset of it, as illustrated in Figure 5(b) of our paper. As an exercise, you could make sure that you don’t create shapes that will never be used. However, even without this additional optimization, a reasonably sized palette only uses a comparatively modest amount of memory (e.g., less than 13MB for the 15x45 palette created above), so our own implementation currently does not bother about this.

Glyph rendering is most efficient when the palette is kept in video memory via vertex buffer objects. [Shr09] or the OpenGL wiki are good places to learn more about the use of vertex buffer objects. All base glyphs share the same index array, so there is no need for more than one index buffer object.

Using Fragment Shaders to Color Code Sign

An efficient and comparatively simple way to achieve the glyph coloring shown in the paper is to evaluate the homogeneous form in a fragment shader. This is simplified by the fact that we transmit the vertex positions of a zero-centered and axis-aligned base geometry to the GPU, and any translation and rotation are done by the modelview matrix.

Our implementation uses the OpenGL Shading Language (GLSL), which is described in the OpenGL documentation. We are using the following GLSL code, which assumes a single directional light source and also does per-pixel Phong shading. Our vertex shader sign.vert is:

varying vec4 diffuse,ambient;
varying vec3 normal,lightDir,halfVector;

void main()
{
  /* transform the normal into eye space and
   * normalize the result */
  normal = normalize(gl_NormalMatrix * gl_Normal);

  /* normalize the (directional) light
   * lights are already in eye space, no need to transform */
  lightDir = normalize(vec3(gl_LightSource[0].position));

  /* Normalize the halfVector (needed in the fragment shader) */
  halfVector = normalize(gl_LightSource[0].halfVector.xyz);

  /* Compute the diffuse, ambient and globalAmbient terms */
  diffuse = gl_Color * gl_FrontMaterial.diffuse * gl_LightSource[0].diffuse;
  ambient = gl_Color * gl_FrontMaterial.ambient * gl_LightSource[0].ambient;
  ambient += gl_Color * gl_LightModel.ambient * gl_FrontMaterial.ambient;

  gl_TexCoord[0] = gl_Vertex; /* pass on vertex pos as tex coordinates */
  gl_Position = ftransform();
}

The corresponding fragment shader sign.frag is:

uniform vec4 posColor,negColor;
uniform vec3 evals;
varying vec4 diffuse,ambient;
varying vec3 normal,lightDir,halfVector;

void main()
{
  vec3 n,halfV;
  float NdotL,NdotHV;

  vec3 v=gl_TexCoord[0].xyz; /* really the untransformed vertex position */
  n = evals*v*v; /* abuse n for evaluating the homogeneous form */
  vec4 signColor=posColor;
  if (n.x+n.y+n.z<0.0)
    signColor=negColor;
  /* The ambient term will always be present */
  vec4 color = ambient*signColor;

  /* re-normalize the interpolated normal */
  n = normalize(normal);

  /* compute the dot product between normal and ldir */
  NdotL = max(dot(n,lightDir),0.0);
  if (NdotL > 0.0) {
    color += diffuse * signColor * NdotL;
    halfV = normalize(halfVector);
    NdotHV = max(dot(n,halfV),0.0);
    color += gl_FrontMaterial.specular *
      gl_LightSource[0].specular *
      pow(NdotHV, gl_FrontMaterial.shininess);
  }

  gl_FragColor = color;
}

Before rendering with these shaders, you will need to set the light source (using standard OpenGL calls, not shown below), specify two glyph colors (one for positive, one for negative), and provide the three eigenvalues of the tensor. Note that in the case where the modelview matrix included the “additional” rotation in our code above, the first and last eigenvalue switch places:

/* setup shaders, once per run of your program: */
const char *vertSource =
#include "sign.vert"
 ;
const char *fragSource =
#include "sign.frag"
 ;
GLhandleARB frag, vert, prog;

frag = glCreateShaderObjectARB(GL_FRAGMENT_SHADER_ARB);
glShaderSourceARB(frag, 1, &fragSource, NULL);
glCompileShaderARB(frag);

vert = glCreateShaderObjectARB(GL_VERTEX_SHADER_ARB);
glShaderSourceARB(vert, 1, &vertSource, NULL);
glCompileShaderARB(vert);

prog = glCreateProgramObjectARB();
glAttachObjectARB(prog, vert);
glAttachObjectARB(prog, frag);
glLinkProgramARB(prog);

/* this can be done once per rendering pass: */
glUseProgramObjectARB(prog);
float posColor[4] = {1.0, 0.38, 0.23,1.0};
float negColor[4] = {0.29, 0.33, 1.0,1.0};
GLint pointer = glGetUniformLocationARB(prog, "posColor");
glUniform4fvARB(pointer,1,posColor);
pointer = glGetUniformLocationARB(prog, "negColor");
glUniform4fvARB(pointer,1,negColor);
pointer = glGetUniformLocationARB(prog, "evals");

/* this needs to be done for each glyph: */
float glevals[3];
if (0==zone || 5==zone || 6==zone || 7==zone || 8==zone) {
   ELL_3V_SET(glevals, evals[2], evals[1], evals[0]);
} else {
   ELL_3V_COPY(glevals, evals);
}
glUniform3fvARB(pointer,1,evals);

To integrate the shader code in this way, you need to encode the above sign.vert and sign.frag as a single C string literal each. On a Unix-style command line,

sed -e 's/^/"/g' < sign.vert | sed -e 's/$/\\n"/g'

should do the trick. If you haven’t worked with shader programs before, we recommend that you consult [RLC09], the official OpenGL documentation and/or online tutorials to gain a better understanding of our sample code, and to find out how to do proper error checking and OpenGL resource management (omitted for brevity).

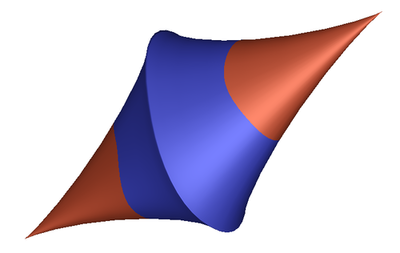
The same glyph geometry as above, but with color coded sign.

References

[RLC09]

(1, 2) Randi J. Rost and Bill Licea-Kane. OpenGL Shading Language (3rd edition). Addison-Wesley, 2009

[Shr09]

(1, 2) Dave Shreiner. OpenGL Programming Guide: The Official Guide to Learning OpenGL, Versions 3.0 and 3.1 (7th edition). Addison-Wesley, 2009.

[SK10]

Thomas Schultz and Gordon Kindlmann. Superquadric Glyphs for Symmetric Second-Order Tensors. IEEE Transactions on Visualization and Computer Graphics (Proc. IEEE Vis) 16(6):1595-1604, 2010.